vol.5 新方式によるバレルめっき2009.10.21
“三隆製作オリジナルのバレル 開放型”
バレルの入口径と胴体部の径の差の部分にワークを投入し、回転しながらめっきを行う。
従来型のバレルと異なり、フタがないことが特徴です。
フタがないことにより、バレル内の亜鉛金属濃度が常に一定に保たれ、また ろ過機の液出口を バレルの入口部分に設置すれば、めっきされているワークの表面には常に新しい液が供給されることになります。
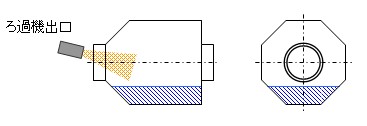
さらに、このバレル内に陽極を設置しました。
従来は、バレルの外側に陽極が設置され、バレル自体が電気抵抗になっていましたが、
バレル内に設置することで、ワークと陽極の間には抵抗となるものがなくなった
のです。
さて 従来、M3のような小ネジは酸性浴を使い、小さなバレルで少量生産を行ってきました。
弊社でも 六角型バレルを用い、酸性浴 ・ 電流密度を低め設定 ・ めっき時間を60分と長くして、 1バレル当たりの投入量40kgのライン を設置したことがあります。
以下に、従来型 酸性浴・六角バレル と 新型 ジンケート浴・開放型バレル補助陽極付 の比較実験結果を記載します。
●六角バレル <酸性浴>
●開放型バレル(補助陽極付) <ジンケート浴>
※黄色表示 : めっき条件が違うもの
●比較実験膜厚測定結果

●比較結果まとめ
六角バレル : 酸性浴
| めっき膜厚理論値 | : 0.535A/dm2×0.285μm×60分 | = 9.1μm |
| 膜厚差 測定位置1(頭部) | : MAX 10.48-MIN 5.35 | = 差 5.13 |
| 膜厚差 測定位置1(軸部) | : MAX 9.05-MIN 3.46 | = 差 5.59 |
| めっき電気使用量 | : 15V×0.664KWA×30台 | = 298.8KWH |
| 生産量 | : 40kg×30 | = 1,200kg |
| 生産量1kg当たりの電気量 | : 298.8KWH÷1200kg | = 0.249KWH/kg |
開放型バレル(補助陽極付) : ジンケート浴
| めっき膜厚理論値 | : 0.35A/dm2×0.285μm×70分 | = 6.98μm |
| 膜厚差 測定位置1(頭部) | : MAX 8.65-MIN 6.54 | = 差 2.11 |
| 膜厚差 測定位置1(軸部) | : MAX 8.12-MIN 5.98 | = 差 2.14 |
| めっき電気使用量 | : 7V×0.430KWA×22台 | =66.22KWH |
| 生産量 | : 40kg×18 | = 720kg |
| 生産量1kg当たりの電気量 | : 66.22KWH÷720kg | = 0.092KWH/kg |
また、従来 酸性浴ではめっき時間が40分程度なのでその場合のテストも行いました。
●<酸性浴>めっき時間40分 開放型バレル
開放型バレル : 酸性浴(40分)
| めっき膜厚理論値 | : 0.8A/dm2×0.285μm×40分 | = 9.12μm |
| 膜厚差 測定位置(頭部) | : MAX 13.26-MIN 6.54 | = 差 6.72 |
| めっき電気使用量 | : 10.75V×0.620KWA×20台 | =133.3KWH |
| 生産量 | : 25kg×30 | = 750kg |
| 生産量1kg当たりの電気量 | : 133.3KWH÷750kg | = 0.178KWH/kg |
この実験データより、酸性浴においては膜厚のバラツキが大きいことがわかると思います。
![]() 注目点!
注目点!
新方式の電気使用量を、従来の方法(六角バレル酸性浴)と比較すると
(新方式) 0.092KWH/kg÷(従来方式) 0.249KWH/kg=36.9%
新方式では、従来方式の 36.9% の電気量で生産が可能です。
1ヶ月に 500t生産した場合の電気使用量を計算すると、差は
生産量1kg当たり 0.249KWH/kg-0.092KWH/kg=0.157KWH/kg
1ヶ月では 500,000kg×0.157KWH=78,500KWH
年間では 78,500KWH×12ヶ月=942,000KHW
1年間で 942,000KWHの差 となります。
この電気使用量をCO2排出量に換算すると、94.2万KWH×4.07=383.4t-CO2
年間 383.4t の二酸化炭素排出量を削減することができます。
原油換算値では、235klの削減量です。
(※ 使用量94.2万KWHを昼間14時間、夜間10時間の割合で換算)
〒434-0046
静岡県浜松市浜名区染地台六丁目5番12号
TEL:053-584-5539(代)
FAX:053-584-5540
最新記事
カテゴリー
月別アーカイブ
- 2024年12月 [2]
- 2024年11月 [1]
- 2024年10月 [3]
- 2024年9月 [4]
- 2024年8月 [2]
- 2024年5月 [1]
- 2024年4月 [2]
- 2024年3月 [3]
- 2024年2月 [7]
- 2024年1月 [11]
- 2023年12月 [8]
- 2023年5月 [1]
- 2023年4月 [2]
- 2023年1月 [1]
- 2021年12月 [1]
- 2021年11月 [2]
- 2021年10月 [3]
- 2021年9月 [2]
- 2021年8月 [2]
- 2021年7月 [4]
- 2021年6月 [5]
- 2021年5月 [4]
- 2021年4月 [4]
- 2021年3月 [5]
- 2021年2月 [2]
- 2021年1月 [2]
- 2020年10月 [3]
- 2020年9月 [4]
- 2020年8月 [2]
- 2020年6月 [1]
- 2019年11月 [2]
- 2019年9月 [3]
- 2019年7月 [2]
- 2019年6月 [3]
- 2019年5月 [2]
- 2019年2月 [1]
- 2019年1月 [3]
- 2018年9月 [1]
- 2018年5月 [1]
- 2018年3月 [2]
- 2018年2月 [2]
- 2018年1月 [3]
- 2017年11月 [1]
- 2017年10月 [2]
- 2017年8月 [1]
- 2017年7月 [4]
- 2017年6月 [1]
- 2017年5月 [3]
- 2017年4月 [2]
- 2017年3月 [1]
- 2017年2月 [1]
- 2017年1月 [2]
- 2016年12月 [3]
- 2016年10月 [2]
- 2016年9月 [3]
- 2016年8月 [1]
- 2016年7月 [4]
- 2016年4月 [1]
- 2016年2月 [1]
- 2015年12月 [1]
- 2015年7月 [1]
- 2015年5月 [1]
- 2015年4月 [4]
- 2015年3月 [1]
- 2015年2月 [1]
- 2015年1月 [1]
- 2014年11月 [1]
- 2014年10月 [4]
- 2014年9月 [4]
- 2014年8月 [4]
- 2014年7月 [2]
- 2014年6月 [1]
- 2014年5月 [1]
- 2014年3月 [1]
- 2014年2月 [1]
- 2014年1月 [1]
- 2013年12月 [1]
- 2013年9月 [2]
- 2013年8月 [1]
- 2013年7月 [2]
- 2013年6月 [1]
- 2013年5月 [1]
- 2013年4月 [2]
- 2013年3月 [2]
- 2013年2月 [2]
- 2013年1月 [2]
- 2012年12月 [1]
- 2012年11月 [4]
- 2012年10月 [3]
- 2012年9月 [2]
- 2012年8月 [2]
- 2012年7月 [2]
- 2012年6月 [2]
- 2012年5月 [3]
- 2012年4月 [2]
- 2012年3月 [2]
- 2012年2月 [2]
- 2012年1月 [2]
- 2011年12月 [2]
- 2011年11月 [2]
- 2011年10月 [1]
- 2011年9月 [2]
- 2011年8月 [1]
- 2011年7月 [2]
- 2011年6月 [3]
- 2011年5月 [2]
- 2011年4月 [3]
- 2011年3月 [2]
- 2011年2月 [2]
- 2011年1月 [2]
- 2010年12月 [3]
- 2010年11月 [1]
- 2010年10月 [2]
- 2010年9月 [2]
- 2010年8月 [1]
- 2010年7月 [3]
- 2010年6月 [2]
- 2010年5月 [1]
- 2010年4月 [1]
- 2010年3月 [4]
- 2010年2月 [4]
- 2010年1月 [3]
- 2009年12月 [3]
- 2009年11月 [3]
- 2009年10月 [3]
- 2009年9月 [2]